
药物设计中的高级计算方法
Subtopic 1: Develop advanced computational methods for drug design
1. Methods for discovering/building proper chemical structures for a given biological target.
2. Methods for predicting the binding affinities of small-molecules to their biological targets.
3. Methods for predicting the key physicochemical properties of organic compounds.
4. Methods for target elucidation based on biological phenotypes.
J. Chem. Inf. Model. 2009, 49, 1079-1093.
Comparative Assessment of Scoring Functions on a Diverse Test Set
Tiejun Cheng, Xun Li, Yan Li, Zhihai Liu, and Renxiao Wang*
Scoring functions are widely applied to the evaluation of protein-ligand binding in structure-based drug design. We have conducted a comparative assessment of 16 popular scoring functions implemented in mainstream commercial software or released by academic research groups. A set of 195 diverse protein-ligand complexes with high-resolution crystal structures and reliable binding constants were selected through a systematic nonredundant sampling of the PDBbind database and used as the primary test set in our study. All scoring functions were evaluated in three aspects, that is, "docking power", "ranking power", and "scoring power", and all evaluations were independent from the context of molecular docking or virtual screening. As for "docking power", six scoring functions, including GOLD::ASP, DS::PLP1, DrugScorePDB, GlideScore-SP, DS::LigScore, and GOLD::ChemScore, achieved success rates over 70% when the acceptance cutoff was root-mean-square deviation < 2.0 Angstrom. Combining these scoring functions into consensus scoring schemes improved the success rates to 80% or even higher. As for "ranking power" and "scoring power", the top four scoring functions on the primary test set were X-Score, DrugScoreCSD, DS::PLP, and SYBYL::ChemScore. They were able to correctly rank the protein-ligand complexes containing the same type of protein with success rates around 50%. Correlation coefficients between the experimental binding constants and the binding scores computed by these scoring functions ranged from 0.545 to 0.644. Besides the primary test set, each scoring function was also tested on four additional test sets, each consisting of a certain number of protein-ligand complexes containing one particular type of protein. Our study serves as an updated benchmark for evaluating the general performance of today's scoring functions. Our results indicate that no single scoring function consistently outperforms others in all three aspects. Thus, it is important in practice to choose the appropriate scoring functions for different purposes.
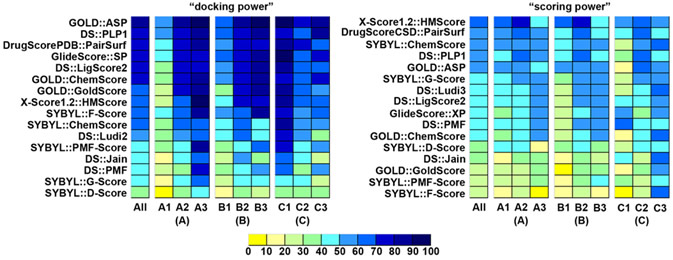
Figure. "Docking power" and "scoring power" of all 16 scoring functions on the subsets in the primary test set. Three sets of subsets were classified by (A) buried percentage of the solvent-accessible surface area of the ligand, (B) buried percentage of the molecular volume of the ligand, and (C) the hydrophobic index of the binding pocket. Here, scoring functions are ranked by their performance on the entire primary test set.
J. Chem. Theory & Comput. 2008, 4, 1959-1973.
Geometrical Preferences of the Hydrogen Bonds on Protein-Ligand Binding Interface Derived from Statistical Surveys and Quantum Mechanics Calculations
Liu, Z. G.; Wang, G. T.; Li, Z. T.; Wang, R. X.*
We have conducted potential of mean force (PMF) analyses to derive the geometrical parameters of various types of hydrogen bonds on protein-ligand binding interface. Our PMF analyses are based on a set of 4535 high-quality protein-ligand complex structures, which are compiled through a systematic mining of the entire Protein Data Bank. Hydrogen bond donor and acceptor atoms are classified into several basic types. Both distance- and angle-dependent statistical potentials are derived for each donor-acceptor pair, from which distance and angle cutoffs are derived in an objective, unambiguous manner. These donor-acceptor pairs are also studied by quantum mechanics (QM) calculations at the MP2/6-311++G** level on model molecules. Comparison of the outcomes of PMF analyses and QM calculations suggest that QM calculation may serve as an alternative approach for characterizing hydrogen bond geometry. Both of our PMF analyses and QM calculations indicate that C-H...O hydrogen bonds are relatively weak as compared to common hydrogen bonds formed between nitrogen and oxygen atoms. A survey on the protein-ligand complex structures in our data set has revealed that CR-H...O hydrogen bonds observed in protein-ligand binding are frequently accompanied by bifurcate N-H...O hydrogen bonds. Thus, the CR-H...O hydrogen bonds in such cases would better be interpreted as secondary interactions.
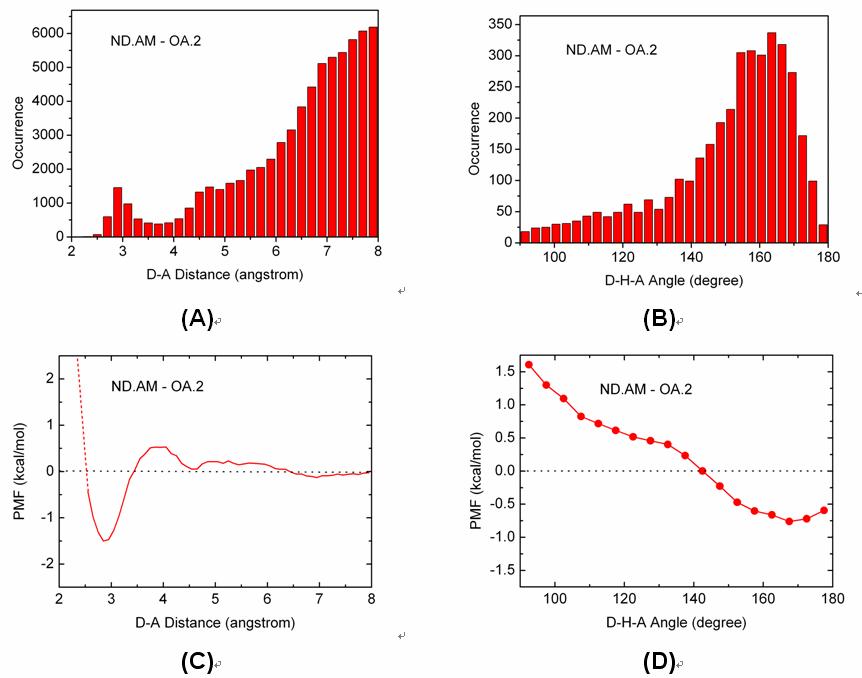
Figure. Distributions of (A) the D-A distances and (B) the D-H-A angles of the ND.AM-OA.2 pair observed on our data set and the corresponding (C) distance-dependent and (D) angle-dependent PMF curves of this hydrogen bonding pair.
J. Chem. Inf. Model. 2007, 47, 2140-2148
Computation of Octanol-Water Partition Coefficients by Guiding an Additive Model
with Knowledge
Tiejun Cheng, Yuan Zhao, Xun Li, Fu Lin, Yong Xu, Xinglong Zhang, Yan Li, Renxiao Wang*and Luhua Lai
We have developed a new method, i.e., XLOGP3, for logP computation. XLOGP3 predicts the logP value of a query compound by using the known logP value of a reference compound as a starting point. The difference in the logP values of the query compound and the reference compound is then estimated by an additive model. The additive model implemented in XLOGP3 uses a total of 87 atom/group types and two correction factors as descriptors. It is calibrated on a training set of 8199 organic compounds with reliable logP data through a multivariate linear regression analysis. For a given query compound, the compound showing the highest structural similarity in the training set will be selected as the reference compound. Structural similarity is quantified based on topological torsion descriptors. XLOGP3 has been tested along with its predecessor, i.e., XLOGP2, as well as several popular logP methods on two independent test sets: one contains 406 small-molecule drugs approved by the FDA and the other contains 219 oligopeptides. On both test sets, XLOGP3 produces more accurate predictions than most of the other methods with average unsigned errors of 0.24-0.51 units. Compared to conventional additive methods, XLOGP3 does not rely on an extensive classification of fragments and correction factors in order to improve accuracy. It is also able to utilize the ever-increasing experimentally measured logP data more effectively.
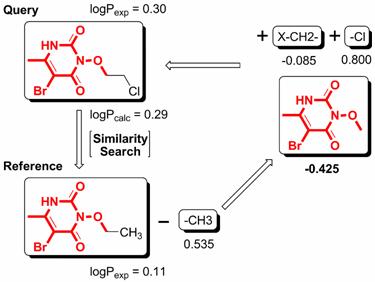
Figure. The basic computational procedure of XLOGP3.
J. Chem. Inf. Model. 2007, 47, 1379-1385
Automatic Perception of Organic Molecules Based on Essential Structural Information
Yuan Zhao, Tiejun Cheng, and Renxiao Wang*
Format conversion is very common in structure preparation in molecular modeling studies. Unfortunately, format conversion cannot always be executed precisely. We have developed an automatic method, called I-interpret (available on-line at http://www.sioc-ccbg.ac.cn/software/I-interpret/), for interpreting the chemical structure of a given organic molecule merely from its essential structural information, including element identities and three-dimensional coordinates of its component atoms. I-interpret uses standard geometrical parameters of organic molecules in atom/bond-type assignment. A series of elaborate considerations are arranged in a logical sequence for this purpose. I-interpret was tested on a set of 179 small organic molecules from the Protein Data Bank and a set of 1990 organic molecules from the NCI diversity set. On both sets, it achieved a success rate of over 95% in interpreting the correct chemical structures, outperforming other programs under our evaluation. I-interpret also provides users some optional functions, which makes it more flexible and powerful in practice. It may serve as a valuable tool for processing chemical structures in molecular modeling.
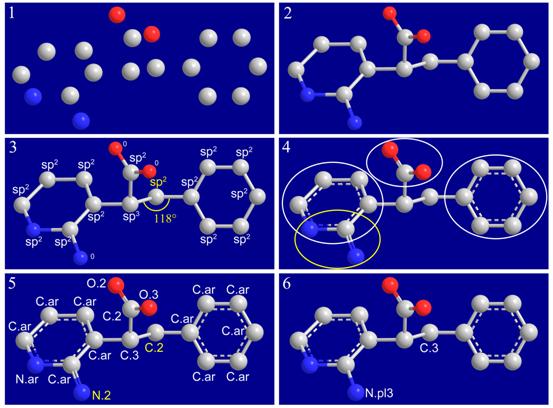
Figure. Interpreting the chemical structure of an organic molecule from nude model. (1) Only identities and threedimensional coordinates of all non-hydrogen atoms are needed as inputs. (2) Covalent connections in the given molecule are established. (3) Hybridization states are assigned to atoms. Terminal atoms remain unresolved until later steps. (4) Functional groups and aromatic rings are identified. (5) All bonds and atoms are resolved. Two conflicts remain in the structure, which are colored in yellow. (6) Conflicts are resolved by resetting certain atom types and bond types.
Journal of Molecular Graphics and Modelling 26 (2007) 368-377
I-SOLV: A new surface-based empirical model for computing solvation free energies
Renxiao Wang *, Fu Lin, Yong Xu, Tiejun Cheng
We have developed a new empirical model, I-SOLV, for computing solvation free energies of neutral organic molecules. It computes the solvation free energy of a solute molecule by summing up the contributions fromits component atoms. The contribution froma certain atomis determined by the solvent-accessible surface area aswell as the surface tension of this atom. Atotal of 49 atomtypes are implemented in ourmodel for classifyingC, N, O, S, P, F, Cl, Br and I in common organic molecules. Their surface tensions are parameterized by using a data set of 532 neutral organic molecules with experimentallymeasured solvation free energies.Ahead-to-head comparison of ourmodel with several other solvationmodels was performed on a test set of 82 molecules.Our model outperformed other solvation models, including widely used PB/SAandGB/SAmodels, with amean unsigned error as low as 0.39 kcal/mol. Our study has demonstrated again that well-developed empirical solvation models are not necessarily less accurate than more sophisticated theoretical models. Empirical models may serve as appealing alternatives due to their simplicity and accuracy.
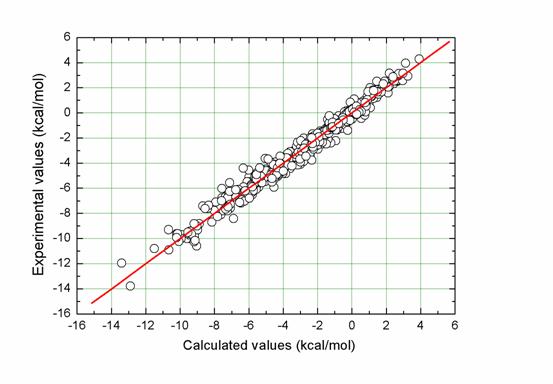
Figure. Correlation between experimentally measured solvation free energies and fitted values by I-SOLV for the entire data set (N = 532, R = 0.989, SD = 0.47 kcal/mol, MUE = 0.35 kcal/mol).
Copyright ©2007-2021 上海盈赛思信息科技有限公司 网站备案号:沪ICP备2021015625号-2 ![]() 沪公网安备:正在申请中
沪公网安备:正在申请中
Technical Support(技术支持): yingsaisi@foxmail.com
